| mind games |
Quentin Heath reveals methods of making computers seem intelligent
SEVERAL MONTHS ago I promised an occasional series of articles about the programming techniques used in such games as chess, battle strategy and adventure. For those who have waited patiently for the series I fulfil the promise.
Every mind game has a definite structure. It is that structure which determines not only how good the game is but also the way in which it plays.
Many types of game have been explored in this column so it will be an interesting exercise to see the techniques in action and will also provide you with an excuse to polish your programming techniques.
The technique which is the most important in artificial intelligence games is tree structuring. It is the structure which is most used and most useful to the chess programmer. It is one way in which data concerning the state of the game and the usefulness of certain moves is contained in the computer. By manipulating the data, the computer will be able to see which move is best to force a win against a human player.
A typical tree is shown in figure one. It has been pruned for the sake of simplicity but as a game of chess is played it would grow longer. The tree is odd-looking because it has a root at the top and branches which creep down towards the bottom of the page. Each circle which connects one branch to another is called a node - a point where a decision has to be taken by the computer. It has to decide which branch it should take next in its quest down to the end of the structure.
Each level of nodes, on a horizontal plane, is called a ply and the first of those starts after the root. The tree in the illustration is only one example of the many arrangements which can be formed by a computer in its quest for the winning move.
The use of a tree is an involved process which only a computer could handle. An average tree can run into hundreds of plys and thousands of nodes. It would take a human several weeks to work through a tree but would take a computer only two seconds, depending on the skill level at which the computer can be set. When a computer game starts, the tree structure does not exist. It is built in the RAM of the machine as the computer plays its strategy. All that exists is the root node at the top of the tree which usually points to the address at which the tree is stored in memory.
Two subroutines must exist in some form in a program, called the legal move generator and the evaluation module. Both units aid the computer to create a tree which will play a winning game.
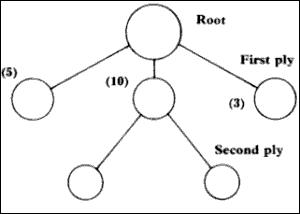
Figure 1. Development of a tree. |
When the computer starts to play, the first thing it seeks is a table of all the possible moves on the board from the legal move generator. The generator finds all the starting moves and produces the first ply of branches from the root of the tree. There may be only a few starting moves, like a game of Nim, or many moves, as in chess, but the computer does not mind. In the fictitious game tree in figure one there are three possible starting positions. They will form the basis for the next move of the computer.
The evaluation module finds which move is closest to the best from all the possible moves. Usually it does so by giving each possible move a score. For instance, in figure one the left-hand node move has been given the score 5, the middle 10 and the right 3. That means that the most promising move is the middle one. The middle node of the first ply then becomes a new root and the computer moves down the tree.
When the evaluator has made its decision, the computer decides whether it has won the game. If it has, it can finish its tree, make the final move and inform the user. If the winning move has not been found, the computer will return to the legal move generator, use the last move root, in the middle, as a root and produce branches again for the possible moves. Once found, those moves will be evaluated as with the first ply and if a winning move is not found, the computer will generate yet another ply of possible moves.
The representation of a tree in the computer memory does not look like that in the diagram. It would be represented as a table of numbers if the game is in machine code, or numbers in an array if the program is in Basic.
You might have guessed that as the computer could create some massive trees the program could run out of computer memory and be unable to continue the game. There is an easy way to circumvent the problem and that is to prune the tree.
The tree search is a heuristic technique. Using it the computer has to learn from its mistakes and make judgements on the data it has collected. There is another type of technique, an algorithm, in which a ready-made solution is built into the program and the computer follows that to the end and a win.
It is done by cutting away the branches of the tree which are no longer important. They would include all nodes before the current root and those branches and nodes which have been eliminated and not continued. The pruning would free space in memory for extra branches and keep the amount of data which the computer has to sort to a minimum. The computer usually will start its pruning procedures after a certain number of plys have been created. That depends on the type of game and more plys would be needed in chess than in Noughts and Crosses or Nim.
As you can see, the tree structure relies heavily on the legal move generator and the evaluation module. It is those parts of a game program which give the computer its strategic playing power and govern the rules by which the computer fights its duel with the human challenger.
In the next of this occasional series I will examine both those subroutines and see how they affect the performance of a computer which is interested in winning. I will also try to find whether the programmer or the computer makes a chess program a champion.
Next month I will step back into the past and investigate the myth of Perseus and Andromeda, as told by Digital Fantasia.